行列の不変量
ここでは正方行列を考える。
初めは対角化可能なものを考えていたが、よく考えたらこの記事の内容は対角化可能でなくても全部成立した。
唯一対角化を使ったのは節 "固有値の基本対称式" だったが、これはジョルダン分解でも同様の結果になる。
そういえば変な形の行列でも似たような議論を展開することはできるんだろうか。
不変量
行列の要素を組み合わせて計算される量で、
相似変換を施しても変わらないものを考える。これを不変量と呼ぶことにする。
その様な量としてトレースと行列式はよく知られている。
\operatorname{tr}[V^{-1} A V] &= \operatorname{tr}[A V V^{-1}] = \operatorname{tr} A, \\
\det(V^{-1} A V) &= (\det V)^{-1} \det A \det V = \det A.
特性方程式
$\operatorname{tr}$ と $\det$ と言えば $2\times 2$ 行列の
特性方程式、またはケーリー・ハミルトンの関係の係数として出てくる。
改めて考えれば、特性方程式の左辺は $\det$ で書かれていて不変量なのだから、その係数は全て不変量になっていなければならない。
$n\times n$ 行列の場合には特性方程式 $\det(\lambda \mathbb{1}_n - A) = 0$ の左辺は $n$ 次多項式なので係数が $n$ 個出てくる (最高次の係数は自明に 1 なので数えない)。
\det (\lambda \mathbb{1}_n - A) &= \lambda^n + \sum_{k=1}^{n} (-1)^k I_n^k[A] \lambda^{n-k}.
\label{eq:characteristic}
これらの $n$ 個の係数 $I_n^k[A]$ は、行列 $A$ から計算される行列 $A$ の不変量である。
係数の符号 $(-1)^k$ は後で都合が良いのでここで導入してしまう。
但し $I_n^k[A]$ を行列要素から計算する表式は面倒である
(数値的には3重対角にしてから3項間漸化式を立ててやれば簡単に求められるが、陽な表式は面倒である)。
固有値の基本対称式
ここで特性方程式の根が固有値を与えることを思い出せば、
$I_n^k[A]$ は固有値の基本対称式になっていると分かる。
特に $I_n^k[A]$ は $k$ 次の基本対称式である。
つまり、固有値を $a_1, \dots, a_n$ として、$e_k$ を $k$ 次の基本対称式とすると、以下のように書かれる。
I_n^k[A] &= e_k(a_1, \dots, a_n).
特に $I_n^1[A] = \sum_{i=1}^n a_i = \operatorname{tr}[A]$ であり
$I_n^n[A] = \prod_{i=1}^n a_i = \det[A]$ である。
改めて考えれば行列の不変量が固有値で書かれるのは当然である。
行列が相似であることは固有値の組が同じであるということと同値なのだから、
行列の不変量は固有値の組から計算されなければならない。
特に固有値の順序に意味があってはならないので対称式となる。
対称式は全て基本対称式の組み合わせで書かれなければならない。
つまり、行列の不変量は全て $I_n^k[A]$ から計算されなければならない。
言わば $I_n^k[A]$ は行列の基本不変量なのである。
因みに別の不変量の生成方法として
$\operatorname{tr}[A^k] = \sum_{i=1}^n (a_i)^n$ を考えることができる。
無限個作ることができるが全て独立な不変量にはならない。
特に最初の $n$ 個までが独立であり、それ以降は最初の $n$ 個の組み合わせで書ける (式 $\eqref{eq:trA-expression}$ で示す)。
更に何れも $n$ 個の基本対称式で書くことができる (対称多項式を基本対称式に分解する機械的なアルゴリズムが存在する)。
それを逆に解けば $I_n^k[A]$ に $\tr A^k$ を使って具体的表式を与えることもできるはずだ。
しかし、この記事では別の経路を使ってその表式を与える (式 $\eqref{eq:invariant-trA-expression}$)。
或いは特性方程式の左辺を、
行列式の微分の公式を使って微分していけば、
やはり何らかの $I_n^k[A]$ の表式が得られよう。
角運動量の分解
角運動量の合成 ($\text{O}(3)$ の既約分解) と関係がある気がしたのでこの記事を書き始めたがやっぱり関係ない。寝ぼけていた。
不変量の表式1 (小行列式)
ここまでは完全に前準備のつもりで、しかし本当に書こうと思っていた内容は消滅してしまった。
収まりが悪いので適当に内容をでっち上げるしかない。
という事で、不変量 $I_n^k[A]$ の具体的な形について考える事にする。
勿論、愚直に行列式の定義を書き下して、無理矢理二項展開して整理すれば何か式が出てくる (附録参照)。
I_n^k[A]
&= \sum_{1 \le \alpha_1 < \dots < \alpha_k \le n}^{_nC_k} \det\bigl[A\bigl(^{\alpha_1 \dots \alpha_k}_{\alpha_1 \dots \alpha_k}\bigr)\bigr].
\label{eq:invariant-raw}
但し、$\sum^{_nC_k}$ は $_nC_k$ 通りある増大列 $(\alpha_1, \dots, \alpha_k)$ についての和である。
$A\bigl(^{\alpha_1 \dots \alpha_k}_{\beta_1 \dots \beta_k}\bigr)$ は
以下のように $A$ の $\alpha_1\dots\alpha_k$ 行目の更に $\beta_1\dots\beta_k$ 列目を取り出して作られた小行列である。
A\bigl(^{\alpha_1 \dots \alpha_k}_{\beta_1 \dots \beta_k}\bigr)
:= \begin{pmatrix}
A_{\alpha_1 \beta_1} & \cdots & A_{\alpha_1 \beta_k} \\
\vdots & \ddots & \vdots \\
A_{\alpha_k \beta_1} & \cdots & A_{\alpha_k \beta_k}
\end{pmatrix}.
不変量の表式2 (リングダイアグラム)
然し、$_nC_k$ 個の小行列式の和というのも余り直観が働かない。
もっと分かりやすい表示はないだろうか。
式 $\eqref{eq:characteristic}$ を見れば $\lambda$ について
$\det (\lambda \mathbb{1}_n - A)$ を逐次微分すれば、
$I_n^n[A],\dots,I_n^1[A]$ を順番に得られることが分かる。
しかし、実際に何回か微分して気付いてしまったが、これはよくある摂動展開である。
なので方針を変えて、手動で微分を犯したことは忘れることにする。
パラメータ $g := 1/\lambda$ を導入すれば
\det (\mathbb{1}_n - gA)
&= g^n \det(\lambda \mathbb{1}_n - A) \\
&= 1 + \sum_{k=1}^{n} (-g)^k I_n^k[A].
となるので、$gA$ についての摂動で係数を求めると都合が良さそうだ。
\det(\mathbb{1}_n - gA)
&= \exp \tr\ln(\mathbb{1}_n - gA) \\
&= \exp\Bigl( -\sum_{l = 1}^\infty \frac1lg^l \tr[A^l] \Bigr) \\
&= \exp\Bigl(\sum_{l = 1}^\infty g^l \cdot \text{($l$-vertex connected ring)} \Bigr) \\
&= \sum_{l = 1}^\infty g^l \cdot \text{($l$-vertex rings)}, \\
\therefore\quad
I_n^l[A]
&= (-1)^l \cdot \text{($l$-vertex rings)}.
\label{eq:invariant-trA-expression}
ファインマン則を一応書いておく。
線には $A$ を割り当て、
頂点には $1$ を割り当てる ($g$ を割り当てたくなるが今回は外に括り出したいので)。
輪一つに対して $(-1)$ を一つ割り当てる。
輪の対称因子は数珠順列ではなくて円順列で考える (裏返し対称性は考えない)。
幾つか具体例を書き下しておく。
I_n^1[A] &= (-1)\left[ \right] = \tr A, \\
I_n^2[A] &= (-1)^2\left[
\right] = \tr A, \\
I_n^2[A] &= (-1)^2\left[ +
+  \right] \\
&= -\frac12\tr A^2 + \frac1{2!}(\tr A)^2 \\
&= \frac12[(\tr A)^2 - \tr A^2], \\
I_n^3[A] &= (-1)^3\left[
\right] \\
&= -\frac12\tr A^2 + \frac1{2!}(\tr A)^2 \\
&= \frac12[(\tr A)^2 - \tr A^2], \\
I_n^3[A] &= (-1)^3\left[
 +
+  +
+  \right] \\
&= -\Bigl[-\frac13\tr A^3 + \frac12\tr A^2 \tr A - \frac1{3!}(\tr A)^3 \Bigr] \\
&= \frac16[(\tr A)^3 + 2\tr A^3 - 3\tr A^2 \tr A], \\
I_n^4[A] &= (-1)^4\left[
\right] \\
&= -\Bigl[-\frac13\tr A^3 + \frac12\tr A^2 \tr A - \frac1{3!}(\tr A)^3 \Bigr] \\
&= \frac16[(\tr A)^3 + 2\tr A^3 - 3\tr A^2 \tr A], \\
I_n^4[A] &= (-1)^4\left[
 +
+ 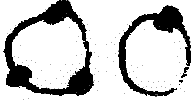 +
+  +
+  +
+  \right] \\
&= \frac1{24}[(\tr A)^4 + 3(\tr A^2)^2 + 8\tr A^3\tr A - 6\tr A^2 (\tr A)^2 - 6 \tr A^4].
\right] \\
&= \frac1{24}[(\tr A)^4 + 3(\tr A^2)^2 + 8\tr A^3\tr A - 6\tr A^2 (\tr A)^2 - 6 \tr A^4].
ここで幾つか気づくことがある。
- 行列の次元 $n$ に依らず $I_n^k[A]$ は $k$ で決まる同じ形の $\tr A^l$ の式で書かれるということ。
- $\det A$ も $\tr A^n$ の多項式で書けるということ。
\det A &= I_n^n[A] = (-1)^n \cdot (\text{$n$-vertex rings}).
- $\det (\mathbb{1}_n - gA)$ が $n$ 次の多項式であることを知っているので、
$l > n$ の時は係数は 0 である。これより、
0 &= (-1)^l \cdot \Bigl[\frac1n\tr A^l + (\text{$l$-vertex disconnected rings})\Bigr], \\
\therefore\quad
\tr A^l &= -n\cdot (\text{$l$-vertex disconnected rings}), \quad (l > n)
\label{eq:trA-expression}
を得るので、再帰的に適用すれば $\tr A^l$ は多項式 $\mathbb{Q}[\tr A, \dots, \tr A^n]$ で書けるということが分かる。
- 実は $\eqref{eq:invariant-trA-expression}$ は、基本対称式 $e_k(a_1, \dots, a_n)$ を
$t_l(a_1, \dots, a_n) = \sum_{i=1}^n (a_i)^l$ で書き表す式とも見られる。
特に、$e_k$ は $t_1,\dots,t_k$ の組み合わせで書ける。
上に挙げたその他の性質も全て対称式の議論に翻訳できる。
不変量の表式3 (逆行列の不変量)
前の節で $\lambda$ で微分することを少し書いたが、すると実は $\tr A^{-k}$ が出てきてしまう。
$g := 1/\lambda$ と置き直したのはそれが理由だった。
同時に、逆行列の不変量 $I_n^k[A^{-1}]$ との関係もあるということに気づく。
\det(\lambda\mathbb{1}_n - A)
&= (-1)^n \det A \cdot\det(1 - \lambda A^{-1}) \\
&= (-1)^n \det A \sum_{k=0}^n (-1)^k \lambda^k I_n^k[A^{-1}] \\
&= \sum_{k=0}^n (-1)^k \det A \cdot I_n^{n-k}[A^{-1}] \lambda^{n-k}. \\
\therefore\quad
I_n^k[A] &= \det A \cdot I_n^{n-k}[A^{-1}].
前の節の式 $\eqref{eq:invariant-trA-expression}$ を用いると、
$k$ が大きい時に輪が物凄くたくさんになって大変である。
$n-k < k$ のときは、こちらの表式を使って $A^{-1}$ に対して、
式 $\eqref{eq:invariant-trA-expression}$ を使った方が項の数が少なくて済む。
例えば、
I_n^{n-1}[A] = \det A \cdot I_n^1[A^{-1}] = \det A \cdot \tr A^{-1}.
附録
式 $\text{\eqref{eq:invariant-raw}}$ の導出を一応書いておく。
\gdef\sgn{\operatorname{sgn}}
\det(\lambda\mathbb{1}_n - A)
&= \frac1{n!} \sum_{\sigma \in \mathfrak{S}_n} \sum_{\tau \in \mathfrak{S}_n} \sgn(\sigma\tau)
\prod_{i=1}^n (\lambda\delta_{\sigma(i),\tau(i)} - A_{\sigma(i),\tau(i)}) \\
&= \frac1{n!} \sum_{\sigma \in \mathfrak{S}_n} \sum_{\tau \in \mathfrak{S}_n} \sgn(\sigma\tau) \nonumber \\
&\quad \times \sum_{k=0}^n _nC_k
\Bigl[\prod_{i=1}^k (- A_{\sigma(i),\tau(i)})\Bigr]
\Bigl[\prod_{i=k+1}^n \lambda\delta_{\sigma(i),\tau(i)}\Bigr] \\
&= \sum_{k=0}^n (-1)^k \lambda^{n-k} I_n^k[A],
I_n^k[A]
&= \frac{_nC_k}{n!}
\sum_{\sigma \in \mathfrak{S}_n} \sum_{\tau \in \mathfrak{S}_n} \sgn(\sigma\tau)
\Bigl[\prod_{i=1}^k A_{\sigma(i),\tau(i)}\Bigr]
\prod_{i=k+1}^n \delta_{\sigma(i),\tau(i)} \\
&= \frac1{k!(n-k)!}
\sum_{\sigma \in \mathfrak{S}_n} \sum_{\rho \in \mathfrak{S}_n} \sgn(\rho)
\Bigl[\prod_{i=1}^k A_{\sigma(i),\sigma(\rho(i))}\Bigr] \nonumber \\
&\quad\times
\prod_{i=k+1}^n \delta_{\sigma(i),\sigma(\rho(i))} \\
&= \frac1{k!(n-k)!}
\sum_{\sigma \in \mathfrak{S}_n} \sum_{\rho \in \mathfrak{S}_k} \sgn(\rho)
\prod_{i=1}^k A_{\sigma(i),\sigma(\rho(i))} \\
&= \frac1{k!(n-k)!} \sum_{\sigma \in \mathfrak{S}_n} \det\bigl[A\bigl(^{\sigma(1)\dots\sigma(k)}_{\sigma(1)\dots\sigma(k)}\bigr)\bigr] \\
&= \sum_{1 \le \alpha_1 < \dots < \alpha_k \le n}^{_nC_k} \det\bigl[A\bigl(^{\alpha_1 \dots \alpha_k}_{\alpha_1 \dots \alpha_k}\bigr)\bigr].\quad\Box
Copyright © 2018, @akinomyoga
Issue
PR
 \right] = \tr A, \\
I_n^2[A] &= (-1)^2\left[
\right] = \tr A, \\
I_n^2[A] &= (-1)^2\left[ +
+  \right] \\
&= -\frac12\tr A^2 + \frac1{2!}(\tr A)^2 \\
&= \frac12[(\tr A)^2 - \tr A^2], \\
I_n^3[A] &= (-1)^3\left[
\right] \\
&= -\frac12\tr A^2 + \frac1{2!}(\tr A)^2 \\
&= \frac12[(\tr A)^2 - \tr A^2], \\
I_n^3[A] &= (-1)^3\left[
 +
+  +
+  \right] \\
&= -\Bigl[-\frac13\tr A^3 + \frac12\tr A^2 \tr A - \frac1{3!}(\tr A)^3 \Bigr] \\
&= \frac16[(\tr A)^3 + 2\tr A^3 - 3\tr A^2 \tr A], \\
I_n^4[A] &= (-1)^4\left[
\right] \\
&= -\Bigl[-\frac13\tr A^3 + \frac12\tr A^2 \tr A - \frac1{3!}(\tr A)^3 \Bigr] \\
&= \frac16[(\tr A)^3 + 2\tr A^3 - 3\tr A^2 \tr A], \\
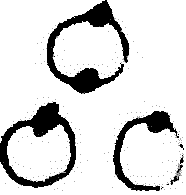
I_n^4[A] &= (-1)^4\left[
 +
+ 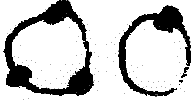 +
+  +
+  +
+  \right] \\
&= \frac1{24}[(\tr A)^4 + 3(\tr A^2)^2 + 8\tr A^3\tr A - 6\tr A^2 (\tr A)^2 - 6 \tr A^4].
\right] \\
&= \frac1{24}[(\tr A)^4 + 3(\tr A^2)^2 + 8\tr A^3\tr A - 6\tr A^2 (\tr A)^2 - 6 \tr A^4].